9663번: N-Queen
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다. N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
문제
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.
N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (1 ≤ N < 15)
출력
첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.
예제 입력 1
8
예제 출력 1
92
풀이
이 문제는 백트레킹으로 해결해야하는 문제이다.
만약 모든 경우의 수에 대해서 재귀를 통해 브루트포스 방식으로 구한다음에 해인지 아닌지를 말단에서 체크하게 되면, DFS가 되는데,
N=8인 경우 체스판의 칸 개수가 8x8=64개이고 이중에 8개를 고르는 조합의 수가 되므로

44억이 넘어갑니다. 이중에 92개만이 정답
가로로 겹치지 않게 한줄에 하나의 queen만 놓는식으로 가지치기(백트래킹)를 하게되면 아래와 같이 줄어듭니다.
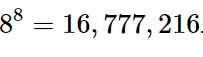
세로로도 겹치지 않게 permutation을 사용하는 백트래킹의 경우 훨씬 더 줄어듭니다.

최종적으로 한줄씩 보면서 가로,세로,대각선 모두에 대해 백트래킹을 사용하면 5,508정도로 더 줄어듭니다.
그렇다면, 확인해야 할 남은 방향은 열기준인 상, 하와 대각선인데 열의 경우 길이가 N인 1차원 배열을 만들어 체크를 해주면 되고,
대각선의 경우, 퀸을 기준으로 ↗, ↙ 이 두 가지 방향은 현재 인덱스의 합이 해당 대각선 방향 각각의 인덱스의 합들과 같다는 규칙이 있었습니다.
(체스판에 직접 인덱스를 매겨서 더해보시면 이해가 쉽습니다. ex) (0,2) = (1,1) = (2,0) )
따라서 2차원 배열을 탐색해가며 겹치는 퀸을 체크하는 것이 아닌 길이가 N * 2 -1인 1차원 배열로 체크가 가능해집니다.
나머지 ↖, ↘ 이 두 방향의 경우도 똑같은 원리로 인덱스 제어 변수가 i, j라고 쳤을 때 i-j+N-1이라는 규칙이 성립합니다.
# 다른 행, 다른 열 이어야함.
n, ans = int(input()), 0
a, b, c = [False]*n, [False]*(2*n-1), [False]*(2*n-1) # a=수직, b=우상향대각선, c=좌상향대각선의 각각 가능한 칸수만큼
def solve(i):
global ans
if i == n: # 퀸을 다 놓았다면
ans += 1 # 경우의 수를 한개 추가
return # 종료
for j in range(n): # 열을 이동하면서
if not (a[j] or b[i+j] or c[i-j+n-1]): # 인덱스의 합과 차가 같다는 것을 이용, 세가지 조건에 부합하지 않는다면
a[j] = b[i+j] = c[i-j+n-1] = True # True 표시
solve(i+1) # 다음 퀸을 놓기 위해 재귀.
a[j] = b[i+j] = c[i-j+n-1] = False # 초기화
solve(0)
print(ans)아직 백트레킹에 대한 개념이 잡히지 않아 다른 분의 풀이를 참고하였습니다.
남의 풀이를 이해하는 것만으로도 시간이 오래 걸려서 조금 찝찝한 기분...
나중에 백트레킹에 대해 집중적으로 공부해야할 필요가 있을 것 같다.
'Algorithm > Online judge' 카테고리의 다른 글
| [백준] 1965번 > 상자 넣기 (0) | 2021.03.02 |
|---|---|
| [백준] 2225번 > 합분해 (0) | 2021.03.02 |
| [백준] 6603번 > 로또 (0) | 2021.03.01 |
| [백준] 11724번 > 연결 요소의 개수 (0) | 2021.03.01 |
| [백준] 1012번 > 유기농 배추 (0) | 2021.03.01 |